"Somewhere deep inside the code, you need to multiply by a number that is less than 1. Thus, we introduce a new factor (1 - σ), where σ must be chosen in a clever way."
Professor Per Christian Hansen laughs, fully aware that the description of a new computational method that he and his colleagues have developed does not make any sense to people without mathematical insight. In fact, it does not sound at all like an exact mathematical solution to a problem. But they can indeed prove that it is.
He himself is most puzzled by how such ideas actually arise:
"It’s like they come from outer space. I can’t force them, simply by sitting at my desk or computer. They might come when I go for a walk, listen to music, or watch a good samurai movie. Afterwards, you must try to prove that the ideas are actually valid."
Reverse mathematics
Per Christian Hansen’s mathematical intuition does not come out of the blue. It is based on knowledge and experience built over a long career. He received his PhD in 1985, and since then he has spent much of his time on solving inverse problems, where - based on measurements - you compute something that you cannot directly see.
The measurements may, for example, come from a CT scanner that sends X-rays through a material sample or a patient. The scanner has sensors that measure how much radiation emerges on the other side, and reverse computations are then made based on these data. This is done via a mathematical model that consists of millions of equations. They are solved on the computer, and the result is a picture of the interior of the sample or the patient.
The equations must be translated into a code that the computer can understand. Solving so many equations obviously takes time, so you occasionally compromise a bit with the exact mathematical formulation to speed up the computations, which may result in a slightly incorrect solution. The calculated image may look OK, but you cannot be sure that it reproduces reality accurately.
Which brings us back to the good idea: Perhaps you could rewrite the code just a little, so that at the same time it does the calculations correctly and runs fast enough. And Per Christian and his colleagues have proved that this actually solves the problem.
Natural mathematical talent
Per Christian Hansen has always had a flair for mathematics, but he was not a prodigy in school. He was bored - the classes were taught too much by the book for his intuitive temperament.
He has always found inverse problems exciting. They trigger his curiosity. And during his studies at DTU he became interested in numerical analysis, which is about translating mathematics into computions.
"It was by chance, like so much else," he says. "I had a really good teacher, Hans Bruun Nielsen, and his way of explaining the subject captured me completely. I loved attending his lectures. It also turned out that I was good at this subject - I could get some original ideas, and this became a self-reinforcing process."
A process that has developed into an impressive career. Per Christian defended his doctoral thesis (habilitation) for the dr.techn. degree in 1996, he is the author or co-author of five books and more than 100 well-cited scientific papers, and he is behind several open source software packages. He has also received several awards, recognitions, and major grants - including one of the prestigious European ERC Advanced Grants of DKK 16 million (for the project HD-Tomo) - and, most recently, a Villum Investigator grant of DKK 35 million.
With the latter, he is now well underway with establishing a major research initiative: Computational Uncertainty Quantification for Inverse Problems, abbreviated CUQI (pronounced 'cookie').
Black hole or cartoon character?
Per Christian Hansen is fascinated by Japan and the country’s strong comic book tradition, and he likes to relax with a good cartoon. In fact, he resorts to a comic book universe when explaining what uncertainty quantification entails.
“It was a big sensation when the first picture of a black hole was presented. And I thought: Is it really a black hole? How certain can we be?,” says Per Christian Hansen, and continues:
“No cameras or measuring systems are faultless. The image may be blurred, noise and vibration may occur during the measurement, and the mathematical models used to go from measurement data to image may contain small inaccuracies. After all, nature is often more complicated than we can express with our formulas.”
“With uncertainty quantification, we can describe and deal with the uncertainty; in this case - which is of course meant as a joke - we determined that the image we have received from space could - with different percentages of probability - be a car tire, a cartoon character, a donut, or a black hole.”
Mathematics with threads to reality
In the CUQI initiative, a rapidly growing team of professors, associate professors, postdocs, PhD students, and visiting researchers are fully immersed in understanding and describing the principles of uncertainty quantification. Per Christian Hansen has no doubt that it will provide useful knowledge:
“We start from an academic point of view, but we must also have links to the real world. When you’ve done some really good mathematics, it is - in fact - very satisfying that someone can actually use it.”
X-ray scans of people or materials are examples of areas where uncertainty quantification is highly relevant, and here the mathematicians in CUQI have already presented results.
When using a CT scanner - to study a patient who needs surgery or a material to be examined for cracks - you rotate the X-ray source or object many times to cover the whole object. However, this may give rise to inaccuracies if you don’t know the exact rotation or geometry.
When we then set up the equations, solve them, and produce a reconstructed image based on what we think are the correct measurement angles, we get - at best - a slightly blurred image. But with uncertainty quantification, we include the inaccuracies in the mathematical model. This gives both a sharper image and an idea of how credible it is.
Per Christian Hansen’s vision is that - by incorporating uncertainty quantifications in the inverse calculations - the user obtains a good approximation to the image and an idea of how large the uncertainties are. The intention is that the new knowledge is turned into a user-friendly software system.
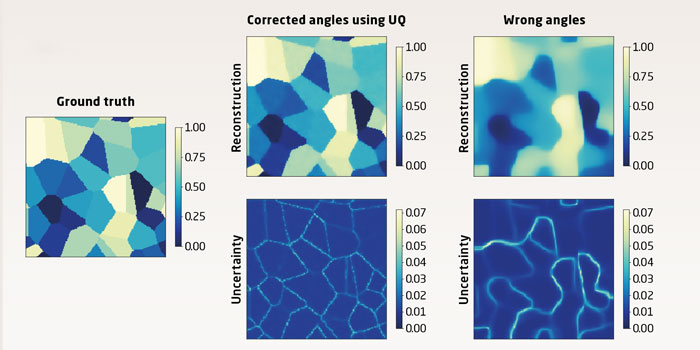
Example of CT reconstruction of the grain structure in a metal. This is a simulation in which we know the ‘ground truth’ precisely. We see two reconstructions together with their uncertainties, partly based on the wrong angles, and partly with the corrected angles based on uncertainty quantification (UQ). The use of UQ provides a much sharper picture with uncertainty in thin stripes on the grain boundaries. The work has been done in collaboration with Associate Professor Yiqiu Dong and Postdoc Felipe Uribe.