”Et sted dybt inde i koden skal man gange med et tal, der er lidt mindre end 1. Derfor introducerer vi en ny faktor (1 - σ), hvor σ skal vælges på snedig vis.”
Professor Per Christian Hansen ler og ved godt, at den beskrivelse af en ny beregningsmetode, som han og hans kolleger har udviklet, ikke giver nogen mening for folk uden matematisk indsigt. Det lyder faktisk slet ikke som en præcis matematisk løsning på et problem. Men det kan de bevise, at det er.
Selv undrer han sig mest over, hvordan sådanne idéer egentlig opstår:
”Det er, som om de kommer ude fra universet. Jeg kan ikke tvinge dem frem ved bare at sætte mig hen til skrivebordet eller computeren. De kommer måske, når jeg går en tur, hører musik eller ser en god samuraifilm. Bagefter må man så se, om man kan bevise, at idéerne holder i virkeligheden.”
Baglæns matematik
Per Christian Hansens matematiske intuition kommer dog ikke helt ud af det blå. Den bygger på viden og erfaring opbygget gennem en lang karriere. Han fik sin ph.d. i 1985, og siden da har hans hjerne en stor del af tiden arbejdet med inverse – omvendte – problemer, hvor man ud fra målinger beregner sig frem til noget, som man ikke direkte kan se.
Målingen kan f.eks. stamme fra en CT-skanner, der sender røntgenstråler igennem en materialeprøve eller en patient. I skanneren sidder nogle sensorer, som måler, hvor meget stråling der kommer ud på den anden side, og ud fra de data regner man baglæns. Man stiller en model op, som består af måske en million ligninger. De bliver løst i en computer, og resultatet er et billede af materialeprøvens eller patientens indre.
Men først skal ligningerne omsættes til kode, som computeren kan forstå. Når den skal løse så mange ligninger, kan det selvfølgelig komme til at tage noget tid, så nogle gange går man lidt på kompromis med den helt præcise matematiske formulering for at speede tempoet op, og det kan resultere i en lidt forkert løsning. Det beregnede billede ser måske fint nok ud, men man kan ikke være sikker på, at det gengiver virkeligheden præcist.
Og så er vi tilbage ved den gode idé: Måske kan man omskrive koden bare en lille smule, så den både gør det rigtigt og kører hurtigt nok. Og det løser faktisk problemet; det har Per Christian og hans kolleger bevist.
Matematisk naturtalent
Per Christian Hansen har altid haft flair for matematik, men han var ikke vidunderdreng i skolen. Undervisningen kedede ham – den foregik for meget efter bogen til hans intuitive temperament.
Han har altid syntes, at inverse problemer er spændende. De trigger hans nysgerrighed. Og i løbet af DTU-studiet blev han sporet ind på numerisk analyse, som handler om at omsætte matematik til computerberegninger.
”Det var som så meget andet en tilfældighed,” fortæller han. ”Jeg havde en rigtig god underviser, Hans Bruun Nielsen, og hans måde at forklare faget på fangede mig fuldstændig. Jeg elskede at komme til hans forelæsninger. Det viste sig også, at jeg var god til det – jeg kunne få nogle originale idéer, og så kørte det derfra i en selvforstærkende proces.”
Og processen udviklede sig til en imponerende karriere. Per Christian har skrevet doktordisputats, er forfatter eller medforfatter til fem bøger og mere end 100 velciterede videnskabelige artikler, og han står bag adskillige open source-softwarepakker. Han har også fået flere priser, anerkendelser og store bevillinger, bl.a. et af de prestigefyldte europæiske ERC Advanced Grants på 16 mio. kr. og senest en Villum Investigator-bevilling på 35 mio. kr.
Med sidstnævnte er han nu i gang med at opbygge et større forskningsinitiativ inden for kvantificering af usikkerhed, Computational Uncertainty Quantification for Inverse Problems, forkortet CUQI (udtalt ’cookie’).
Sort hul eller tegneseriefigur?
Per Christian Hansen er fascineret af Japan og deres stærke tegneserietradition, og han slapper gerne af med en god tegnefilm. Det er også tegneserieuniverset, han tyr til, når han skal forklare, hvad uncertainty quantification går ud på.
”Det var en stor sensation, da man præsenterede det første billede af et sort hul. Men jeg tænkte: Er det nu også et sort hul? Hvor sikre kan vi være på det?,” siger Per Christian Hansen, og fortsætter:
”Ingen kameraer eller målesystemer er fejlfrie. Billedet kan være uskarpt, og der kan opstå støj og rystelser under målingen, og de matematiske modeller, man bruger for at gå fra måledata til billede, kan rumme små unøjagtigheder. Naturen er trods alt ofte mere indviklet, end vi kan udtrykke med vores formler.”
”Med uncertainty quantification sætter vi tal på usikkerheden; i dette tilfælde – der selvfølgelig er ment som en joke – har vi altså beregnet, at det billede, vi har fået fra rummet, med forskellige procents sandsynlighed kunne være et bildæk, en donut, en tegneseriefigur eller et sort hul.”
Matematik med tråde til virkeligheden
I CUQI-initiativet er et hastigt voksende team af professorer, lektorer, postdocs, ph.d.-studerende og gæsteforskere nu i fuld gang med at forstå og beskrive principperne for usikkerhedskvantificering, og Per Christian Hansen er ikke i tvivl om, at det kan blive nyttig viden:
”Vi starter fra et rent akademisk udgangspunkt, men skal også have tråde ud i den virkelige verden. Når man har lavet noget virkelig god matematik, er det jo meget tilfredsstillende, at der også er nogen, der kan bruge det.”
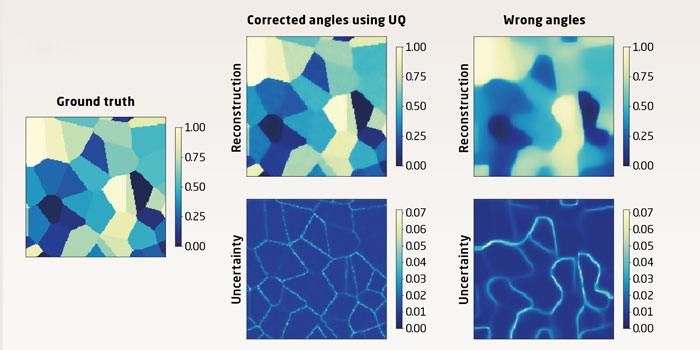
Eksempel på CT-rekonstruktion af korn-strukturen i et metal. Dette er en simulering, således at vi kender ”ground truth” præcist. Vi ser to rekonstruktioner sammen med deres usikkerheder, dels baseret på de forkerte vinkler, og dels med de korrigerede vinker baseret på undertainty quantification (UQ). Brugen af UQ giver et meget skarpere billede med usikkerhed i tynde striber på korngrænserne. Arbejdet er lavet i samarbejde med lektor Yiqiu Dong og postdoc Felipe Uribe.
Røntgenskanninger af personer eller materialer er eksempler på områder, hvor usikkerhedskvantificeringer vil være yderst relevante, og her har matematikerne i CUQI allerede præsenteret resultater (se figur).
Når man bruger CT-skanning – det kan være af en patient, der måske skal opereres, eller et materiale, der skal undersøges for revner – er man nødt til at dreje røntgenkilden eller materialet mange gange for at få hele området dækket. Men dermed kan der opstå unøjagtigheder, hvis man ikke kender den præcise rotation eller position.
Når man så stiller ligningerne op, løser dem og laver et rekonstrueret billede ud fra de vinkler, man tror, er de rigtige, får man i bedste fald et lidt uskarpt billede. Men med uncertainty quantification medtager man unøjagtighederne i den matematiske model. Dermed får man både et skarpere billede og en idé om, hvor troværdigt det er.
Per Christian Hansens vision er, at man ved at bringe usikkerhedskvantificeringer ind i de inverse beregninger på én gang kan give brugeren et godt bud på billedet og en idé om, hvor store usikkerhederne er, og det er meningen, at den nye viden efterhånden skal samles i et brugervenligt softwaresystem.